RELLENO DE POLÍGONOS
Polígono es una figura básica dentro de las representaciones y tratamiento de imágenes bidimencionales y su utilización es muy interesante para modelar objetos del mundo real.
En un sentido amplio, se define como una región del espacio delimitada por un conjunto de lineas (aristas) y cuyo interior puede estar rellenado por un color o patrón dado.
CASOS DE RELLENO SEGÚN SU COMPLEJIDAD
El caso mas sencillo de relleno es el triangulo.
Luego sigue el relleno de polígonos convexos de N-lados.
Relleno de polígonos cóncavos.
MÉTODO DE RELLENO DE POLÍGONOS CON COLOR
- SCAN-LINE
- INUNDACIÓN
- FUERZA BRUTA
- PATRÓN
SCAN-LINE
Fila a fila van trazando lineas de color entre aristas.
- para scan-line que cruce el polígono se busca en la intersección entre las lineas de barrido y las aristas del polígono.
- Dichas intersecciones se ordenan y se rellenan a pares.
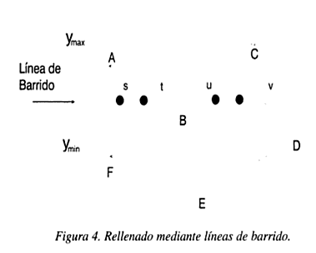
LINEA DE BARRIDO
Es valido para polígonos cóncavos como convexos. Incluso para si el objeto tiene huecos interiores.
Funcionan en el trozo de lineas horizontales, denominadas lineas de barridos, que intersectan un numero de veces, permitiendo a partir de ella identificar los puntos que se consideran interiores al polígono.
INUNDACIÓN
- Empieza en un interior y pinta hasta encontrar la frontera del objeto.
- Partimos de un punto inicial (x,y), un colo de relleno y un color de frontera.
- El algoritmo va testeando los píxeles vecinos a los ya pintados, viendo si son frontera o no.
- No solo sirven para polígonos, sino para cualquier área curva para cualquier imagen AE se usan los programas de dibujo.
FUERZA BRUTA
- Calcula una caja contenedora del objeto.
- Hace un barrido interno de la caja para comprobar c/pixel este dentro del polígono.
- Con polígonos simétricos basta con que hagamos un solo barrido en una sección y replicar los demás pixeles.
- Requiere aritmética punto-flotante, esto lo hace preciso y costoso.
RELLENO MEDIANTE UN PATRÓN
Un patrón viene definido por el área rectangular en el que cada punto tiene determinado color o novel de gris. Este patrón debe repetirse de modo periódico dentro de la región a rellenar. Para ello debemos establecer una relación entre los puntos del patrón y los pixeles de la figura. En definitiva debemos determinar la situación inicial del patrón respecto a la figura de tal forma que podamos establecer una correspondencia entre los pixeles interiores al polígono y los puntos del patrón.
ALTERNATIVAS PARA LA SITUACIÓN INICIAL DEL PATRÓN
Consiste en situar el punto asociado a la esquina superior izquierda del patrón en un vértice del polígono.
- Considerar la región a rellenar en toda la pantalla y por lo tanto el patrón se citua en el origen de esta (esquina superior izquierda).
EJEMPLO DE SCAN-LINE
- Encontrar las intersecciones de los scanlines en el polígono.
- Almacenar las intersecciones en alguna estructura de datos ET (edge table), de manera ordena ascendiente en Y y en X en buckets.
- Rellenar los spans usando la estructura.
- Usar algún criterio de paridad para saber cuando un intervalo debe ser rellenado o no.
Entendemos por modelo de iluminación el cálculo de la intensidad de cada punto de la escena.
En el cálculo de la intensidad de un punto intervienen:
- El tipo e intensidad de la fuente de luz
- El material del objeto
- La orientación del objeto con respecto a la luz
El modelo más utilizado es el modelo de Phong.
PROCESO DE ILUMINACIÓN

- Si un rayo de luz entra al ojo directamente de la fuente, se verá el color de la fuente.
- Si un rayo de luz pega en una superficie que es visible al observador, el color visto se basará en la interacción entre la fuente y el material de la superficie: se verá el color de la luz reflejado de la superficie a los ojos.
En término de gráfica por computadora, se reemplaza el observador por el plano de proyección, como se ve en la siguiente figura:
El recorte del plano de proyección y su mapeo a la pantalla significa un número particular de pixeles de despliegue.
El color de la fuente de luz y las superficies determina el color de uno o mas pixeles en el frame buffer.
Se debe considerar solo aquellos rayos que dejan las fuentes y llegan al ojo del observador, el COP, después de pasar por el rectángulo de recorte.
Cuando la luz da en una superficie, parte se absorbe, y parte se refleja.
- Si la superficie es opaca, reflexión y absorción significará de toda la luz que dé en la superficie.
- Si la superficie es translúcida, parte de la luz será transmitida a través del material y podrá luego interactuar con otros objetos.
Un objeto iluminado por luz blanca se ve rojo porque absorbe la mayoría de la luz incidente pero refleja luz en el rango rojo de frecuencias.
Un objeto relumbrante se ve así porque su superficie es regular, al contrario de las superficies irregulares.
El sombreado de los objetos también depende de la orientación de las superficies, caracterizado por el vector normal a cada punto.


La luz puede dejar una superficie mediante dos procesos fundamentales:
Normalmente se piensa en una fuente de luz como un objeto que emite luz solo mediante fuentes de energía internas, sin embargo, una fuente de luz, como un foco, puede reflejar alguna luz incidente a esta del ambiente.

Aquí, La puede ser cualquiera de las fuentes de luz individuales, o puede el término ambiente global.



INTERACCIONES ENTRE LUZ Y MATERIALES
- Superficies especulares
- Superficies Difusas
- Superficies difusas perfectas
- Superficies translucidas

FUENTES DE LUZ

La luz puede dejar una superficie mediante dos procesos fundamentales:
- Emisión propia
- Reflexión
Normalmente se piensa en una fuente de luz como un objeto que emite luz solo mediante fuentes de energía internas, sin embargo, una fuente de luz, como un foco, puede reflejar alguna luz incidente a esta del ambiente.
Si se considera una fuente como en la siguiente figura, se le puede ver como un objeto con una superficie.
FUNCIÓN DE ILUMINACIÓN
Cada punto (x,y,z) en la superficie puede emitir luz que se caracteriza por su dirección de emisión (θ,Φ) y la intensidad de energía emitida en cada frecuencia λ. Por lo tanto, una fuente de luz general se puede caracterizar por la función de iluminación I(x, y, z, θ,Φ, λ) de seis variables.
Para una fuente de luz distribuida, como un foco de luz, la evaluación de este integral es difícil, usando métodos analíticos I numéricos.
A menudo, es mas fácil modelar la fuente distribuida con polígonos, cada una de las cuales es una fuente simple, o aproximando a un conjunto de fuentes de punto.
Se considerarán cuatro tipos básicos de fuentes, que serán suficientes para generar las escenas más sencillas:
2) Fuentes de punto
3) Spotlights
( Luces direccionales)
4) Luces distantes
MODELO DE ILUMINACIÓN PHONG
Es un modelo empírico simplificado para iluminar puntos de una escena
- Los resultados son muy buenos en la mayoría de las escenas
- En este modelo, los objetos no emiten luz, sólo reflejan la luz que les llega de las fuentes de luz o reflejada de otros objetos
El modelo usa cuatro vectores para calcular el color para un punto arbitrario p sobre la superficie.
Si la superficie es curva, los cuatro vectores pueden cambiar según se mueve de punto a punto.


- El vector n es la normal en p.
- El vector v tiene dirección de p al observador o COP.
- El vector l tiene dirección de una línea de p a un punto arbitrario sobre la superficie para una fuente de luz distribuida, o una fuente de luz de punto.
- El vector r tiene la dirección de un rayo perfectamente reflejado de l. La dirección de r está determinada por n y l.
El modelo Phong apoya los tres tipos de interacciones material-luz: ambiente, difusa y especular. Si se tiene un conjunto de fuentes puntos, con componentes independientes para cada uno de los tres colores primarios para cada uno de los tres tipos de interacciones material- luz; entonces, se puede describir la matriz de iluminación para una fuente de luz i para cada punto p sobre una superficie, mediante:

- La primera fila contiene las intensidades ambiente para rojo, verde y azul para la fuente i.
- La segunda fila contiene los términos difusos.
- La tercera fila contiene los términos especulares. (Aún no se ha aplicado ninguna atenuación por la distancia.)
REFLEXION DE AMBIENTE
La intensidad de la luz ambiente La es la misma sobre cada punto de la superficie. Parte de la luz es absorbida y parte es reflejada. La cantidad reflejada está dada por el coeficiente de reflexión de ambiente ka, Ra = ka. Como sólo se refleja una fracción positiva de luz, se debe tener
0 ≤ ka≤ 1
y por lo tanto
Ia= kaLa
Aquí, La puede ser cualquiera de las fuentes de luz individuales, o puede el término ambiente global.
Una superficie tiene tres coeficientes ambiente, kar, kag y kab, que pueden ser distintas. Por ejemplo, una esfera se vería amarilla bajo luz ambiente blanca si su coeficiente ambiente azul es pequeño y sus coeficientes rojo y verde son grandes.
EJEMPLO:
EJEMPLO:

REFLEXION DIFUSA
Un reflector difuso perfecto esparce la luz que refleja de manera igual en todas las direcciones, viéndose igual para todos los observadores. Sin embargo, la cantidad de luz reflejada depende del material, dado que parte de la luz es absorbida, y de la posición de la fuente de luz relativa a la superficie. Reflexiones difusas son caracterizadas por superficies rugosas, como se ve en la siguiente figura (corte trasversal):


Se considera una superficie plana difusa iluminada por el sol, como se muestra en la siguiente figura:


La superficie se vuelve mas brillante al mediodía, y menos durante la madrugada y la puesta, dado que, según la ley de Lambert, solo se ve el componente vertical de la luz entrante. Para comprender esta ley, se considera una fuente de luz paralela pequeña pegando en un plano, como se muestra en la siguiente figura:

Según la fuente baja en el cielo (Artificial), la misma cantidad de luz se esparce sobre una área mas grande, y la superficie parece oscurecerse.
Se puede caracterizar reflexiones difusas matemáticamente. La ley de Lambert dice que:
Rd ∝ cosθ
Donde θ es el ángulo entre la normal n en el punto de interés y la dirección de la fuente de luz l. Si l y n son ambos vectores unidad, entonces
cosθ = l ⋅ n
Si se agrega un coeficiente de reflexión kd que representa la fracción de luz difusa entrante que es reflejada, se tiene el siguiente término de reflexión
Id= kd (l ⋅ n) Ld 0 ≤ kd≤ 1
Si se desea incorporar el término de distancia, para considerar la atenuación de la luz según esta viaja una distancia d desde la fuente a la superficie, se puede agregar el término cuadrático de atenuación:
EJEMPLO:
REFLEXION ESPECULAR
Si se emplea solo reflexiones ambiente y difusas, las imágenes serán sombreadas y aparecerán tridimensionales, pero todas las superficies se verán sin vida. Lo que hace falta son la reflexión de secciones más brillantes en los objetos. Esto ocasiona un color diferente del color del ambiente reflejado y luz difusa. Una esfera roja, bajo luz blanca, tendrá un resplandecer blanco que es la reflexión de parte de la luz de la fuente en la dirección del observador.
Mientras que una superficie difusa es rugosa, una superficie especular es suave. Mientras mas lisa se la superficie, mas se parece a un espejo, como se ve en la siguiente figura.
Según la superficie se hace mas lisa, la luz reflejada se concentra en un rango mas pequeño de ángulos, centrado alrededor del ángulo de un reflector perfecto: un espejo o una superficie especular perfecta. Modelar superficies especulares realísticas puede ser complejo, ya que el patrón por el cual se esparce no es simétrico, dependiendo de el largo de onda de la luz incidente y cambia con el ángulo de reflexión
Phong propuso un modelo aproximado que puede computarse con solo un pequeño incremento en el trabajo para superficies difusas. El modelo agrega un término para reflexión especular. Se considera la superficie como rugosa para el término difuso u lisa para el término especular. La cantidad de luz que el observador ve depende del ángulo ø entre r, la dirección de un reflector perfecto, y v, la dirección del observador. El modelo de Phong usa la ecuación
Is= ks Ls cosα φ 0 ≤ ks ≤ 1
El coeficiente ks (0 ≤ ks ≤ 1) es la fracción reflejada de la luz especular entrante. El exponente α es el coeficiente de brillantez.
La siguiente figura muestra como, según se incrementa a, la luz reflejada se concentra en una región mas delgada, centrada en el ángulo de un reflector perfecto.
La siguiente figura muestra como, según se incrementa a, la luz reflejada se concentra en una región mas delgada, centrada en el ángulo de un reflector perfecto.
En el límite, según α tiende a infinito, se obtiene un espejo; valores entre 100 y 500 corresponden a la mayoría de las superficies metálicas, y valores menores (<100) corresponden a materiales que muestran brillantez gruesa.
La ventaja computacional del modelo de Phong es que, si se normaliza r y v a valores unitarios, se puede usar el producto punto, y el término especular se vuelve
Se puede agregar el término de distancia, como se hizo con las reflexiones difusas. Finalmente, se refiere al modelo Phong, incluyendo el término de distancia, a la siguiente ecuación:
Esta fórmula se computa para cada fuente de luz y para cada primaria.
El modelo de Phong se ha hecho en espacio de objetos. El sombreado, sin embargo, no se hace hasta que los objetos hayan pasado por las transformaciones modelo-vista y proyección. Estas transformaciones pueden afectar los términos de coseno en el modelo.
EJEMPLO:
EJEMPLO:

TÉCNICAS DE SOMBREADO
Sombra
Una sombra es una región
de oscuridad donde la luz es obstaculizada. Una sombra
ocupa todo el espacio detrás de un objeto opaco con una fuente de luz frente a él.
La sección eficaz de una sombra es
una silueta bidimensional o una proyección invertida
del objeto que aspira la luz.
Sombras
de colores
Si sólo existe una fuente de luz,
las sombras arrojadas por aquella serán siempre grises, sea cual sea el color
de la fuente. En cambio, si existen dos fuentes de luz de distintos colores,
supongamos rojo y azul, las sombras proyectadas por cada una de ellas serán del
color de la otra fuente de y sólo la intersección de ambas sombras será gris.
Es decir, la sombra de la luz roja será azul, pues está iluminada por la fuente
azul, y viceversa.
SOMBREADO
El
sombreado es una práctica común entre los artistas. Este puede ser usado para
crear sombras, textura o
una formación de un objeto dentro de una imagen.
INTENSIDAD CONSTANTE
EN CIERTAS CONDICIONES, UN OBJETO
CON SUPERFICIES PLANAS PUEDE SOMBREARSE EN FORMA REALISTA UTILIZANDO
INTENSIDADES DE SUPERFICIE CONSTANTES. EN EL CASO DONDE UNA SUPERFICIE SE
EXPONE SOLAMENTE A LA LUZ AMBIENTE Y NO SE APLICAN DISEÑOS, TEXTURAS O SOMBRAS
DE SUPERFICIE, EL SOMBREADO CONSTANTE GENERA UN A REPRESENTACIÓN EXACTA DE LA
SUPERFICIE.
UNA SUPERFICIE CURVA QUE SE
REPRESENTA COMO UN CONJUNTO DE SUPERFICIES PLANAS PUEDE SOMBREARSE CON
INTENSIDADES DE SUPERFICIE CONSTANTE, SI LOS PLANOS SE SUBDIVIDEN LA SUPERFICIE
SE HACE LO SUFICIENTEMENTE PEQUEÑOS.
SOMBREADO DE GOURAUD
ESTE ESQUEMA DE INTERPOLACIÓN DE
INTENSIDAD, CREADO POR GOURAUD, ELIMINA DISCONTINUIDADES EN INTENSIDADES ENTRE
PLANOS ADYACENTES DE LA REPRESENTACIÓN DE UNA SUPERFICIE VARIANDO EN
FORMA LINEAL LA INTENSIDAD SOBRE CADA PLANO DE MANERA QUE LO VALORES DE LA
INTENSIDAD CONCUERDEN EN LAS FRONTERAS DEL PLANO. EN ESTE MÉTODO LOS VALORES DE
LA INTENSIDAD A LO LARGO DE CADA LÍNEA DE RASTREO QUE ATRAVIESAN UNA SUPERFICIE
SE INTERPOLAN A PARTIR DE LAS INTENSIDADES EN LOS PUNTOS DE INTERSECCIÓN DE
CON LA SUPERFICIE.
SOMBREADO DE PHONG
EL SOMBREADO DE PHONG PRIMERO
INTERPOLA LOS VECTORES NORMALES EN LOS PUNTOS LIMITE DE UNA LÍNEA DE RASTREO.
PUEDE HACERSE MEJORAS A LOS MODELOS DE SOMBREADO DE GOURAUD DETERMINANDO LA
NORMAL APROXIMADA A LA SUPERFICIE EN CADA PUNTO A LO LARGO DE UNA LÍNEA DE
RASTREO Y CALCULANDO DESPUÉS LA INTENSIDAD MEDIANTE EL USO DEL VECTOR NORMAL
APROXIMADO EN ESE PUNTO.
ALGORITMO DE TRAZO DE RAYAS
ES UN BUEN MÉTODO PARA DETERMINAR LAS
INTENSIDADES ESPECULARES EN POSICIONES VISIBLES DE LA SUPERFICIE CONSISTE EN
TRAZAR RAYAS HACIA ATRÁS DESDE LA POSICIÓN DE VISIÓN HASTA LA FUENTE DE LUZ.
COMENZANDO DESDE LA POSICIÓN DE
VISIÓN, LA RAYA QUE ATRAVIESA CADA PIXEL EN EL PLANO DE VISIÓN SE TRAZA HACIA
ATRÁS A UNA SUPERFICIE DE LA ESCENA TRIDIMENSIONAL. ESTA TÉCNICA, CONOCIDA COMO
TRAZO DE RAYAS
Con todas estas técnicas la calidad de las imágenes son mejores y ayudan a entender de mejor manera su entorno y condiciones que tienen cada una de ella para poder así tener un aspecto mas realista de nuestro mundo real.
























No hay comentarios.:
Publicar un comentario